Pruning: The History And Overview

Definition

Simply speaking, pruning is a process of shrinking a network by eliminating parameters.

Formally, let’s define a neural network architecture is as a family of functions \(f(x; ·)\). By using a model \(f(x; W)\) as input, a new model \(f(x; M \bigodot W')\) is created via neural network pruning.

Here,

\(M \in {0, 1} ^ { \vert W' \vert }\) is a binary mask that sets certain parameters of the model to \(0\).
\(W′\) is a collection of parameters that might be different from \(W\).
\(\bigodot\) is the elementwise product operator.

In production, trimmed parameters of \(W\) are either set to zero or eliminated totally, rather than employing an explicit mask.

History

The pruning has been used since the late 1980s. Among the most famous publications of those years, LeCun et al. (1989). Optimal Brain Damage, Karnin. (1990) A simple procedure for pruning back-propagation trained neural networks and Hassibi et al. (1993). Optimal Brain Surgeon and general network pruning.

First methods in pruning assumed brute-forcing for every weight, setting it to zero and evaluating the change in the error. It is a very non-optimal \(O(MW^3)\) algorithm, where \(W\) is the nubmer of weights and \(M\) is training simple operations. See the amazing survey Reed. (1993). Pruning Algorithms – A Survey for more details about 80s - 90s pruning algorithms.

According to Semantic Scholar, across the most influenced papers in pruning nowadays are Han et at. (2015). Deep Compression: Compressing Deep Neural Network with Pruning, Trained Quantization and Huffman Coding, Li et at. (2016). Pruning Filters for Efficient ConvNets and He et at. (2017). Channel Pruning for Accelerating Very Deep Neural Networks.

Given the high interest in neural network pruning during the last few years, it seems only appropriate to investigate about the relative effectiveness of various pruning methods. The methods vary in how many parameters should be pruned, which one to prune, when to prune and how to fine-tune the model after the pruning. See Blalock et al. (2020). What is the State of Neural Network Pruning? for the review of the pruning methods by 2020.

Why Pruning?

Most publications about the pruning include at least one of these two metrics:

the number of FLOPs, needed to do inference using the pruned network.
the number of model parameters, that were removed.

Actually, there are more pros than we see now. Namely?

The model’s storage footprint, device’s memory consumption, inference computing costs, inference energy usage, etc. are all impacted by reducing the number of model parameters.

By adding tiny amounts of compression during pruning, the model’s accuracy may occasionally even be increased (probably because of regularization effect, see Suzuki et al. (2018). Spectral Pruning: Compressing Deep Neural Networks via Spectral Analysis and its Generalization Error for more details).

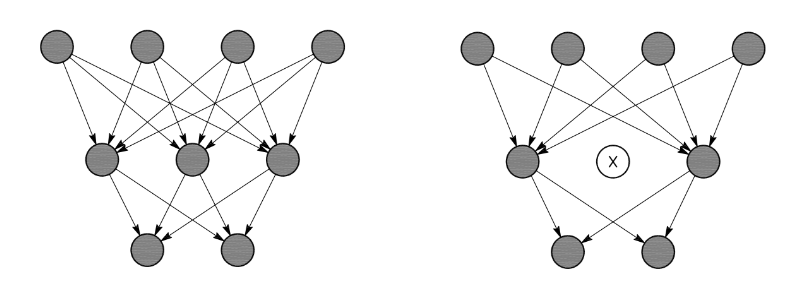
Pruning (**Spec-ResA** model) increased the accuracy on ImageNet

Also, there is a hypothesis, that sparse models tend to outperform dense ones for a fixed number of parameters.

Pruning Methods

The majority of neural network pruning techniques are based on the algorithm below:

def prune_and_finetune(N: int, X: int):
    '''
    Input:
        N is the number of iterations of pruning
        X is the dataset on which to train and fine-tune
    Return:
        M is the mask of 0 and 1, with the size |W|
        W is the final model weights, fine-tuned after pruning
    '''

    # model weights
    W = initialize()

    # f is a training function
    W = train_to_convergence(f, X, W)

    # M is a mask of 0 and 1, with the size |W|
    M = generate_mask(W)

    # do N iterations of pruning
    for i in range(1, N):

        # Each parameter or structural element in the network is given a score s from S,
        # and the network is pruned based on these scores.
        S = score(W)

        # prune the model, applying binary mask M according to the S score
        M = prune(M, score(W))

        # fine-tune the model after pruning
        W = fine_tune(f, X, M, W)

    return M, W

The network is initially trained to convergence in this algorithm. After that, a score is assigned to each parameter or structural component in the network, and the network is pruned in accordance with these scores. The network must be further trained (referred to as “fine-tuning”) to recover when pruning affects its accuracy. The network’s size is steadily decreased by a series of pruning and fine-tuning iterations.

Various questions need different model pruning techniques, which should be answered. Before you prune, you should consider the following key questions.

Which structure should we prune?
- Unstructured pruning. Individual weights are pruned via unstructured pruning, which ignores their location inside each tensor. [LeCun et al. (1989), Han et at. (2015)]
- Structured pruning. Convolutional filters, channels, or weights can all be removed as part of structured pruning. [Li et at. (2016)]
When pruning should be applied?
- Regularization and gradual pruning. The network is pruned during the training process, resulting in a pruned network at the end of training. [Louizos et at. (2017)]
- Retraining. Prunes after the training. In order to restore accuracy, the pruned network is often retrained or fine-tuned. [Han et at. (2015)]
Which weights should we prune?
- Global Magnitude Pruning. Prunes the weights all through the network that have the lowest absolute value.
- Layerwise Magnitude Pruning. For each layer of the model, prunes the weights with the lowest absolute value.
- Global Gradient Magnitude Pruning. Prunes the individual weights that, after a batch of inputs has been evaluated, have the lowest absolute value of \(\text{weight} * \text{gradient}\).
- Layerwise Gradient Magnitude Pruning. Prunes the entire layer weights that, after a batch of inputs has been evaluated, has the lowest absolute value of \(\text{weight} * \text{gradient}\).
- Random Pruning. Individually prunes each weight with a probability equal to the amount of the network that has to be pruned.

Practical Usage

The most popular libraries for pruning:

he-y/Awesome-Pruning – A curated list of neural network pruning resources.
openvinotoolkit/nncf – Neural Network Compression Framework for enhanced OpenVINO™ inference
neuralmagic/sparseml – Libraries for applying sparsification recipes to neural networks with a few lines of code, enabling faster and smaller models
alibaba/TinyNeuralNetwork – TinyNeuralNetwork is an efficient and easy-to-use deep learning model compression framework.
intel/neural-compressor – An open-source Python library supporting popular model compression techniques on all mainstream deep learning frameworks (TensorFlow, PyTorch, ONNX Runtime, and MXNet).